Jika anda telah memahami konsep dasar integral yaitu integral tak tentu dan integral tentu. Anda akan mungkin lebih mudah dalam mempelajari aplikasi dari integral. Aplikasi integral yang biasanya dipelajari adalah penerapan integral dalam menghitung luas daerah yang dibatasi oleh kurva dan penggunaan integral untuk menentukan volume benda putar.
Pada bahasan kali ini kita akan membahas mengenai aplikasi integral untuk menghitung luas daerah. Luas daerah yang dimaksud dalam hal ini adalah luas daerah yang dibatasi oleh kurva dengan sumbu x dan luas daerah yang dibatasi oleh dua kurva
Misalkan kurva y = f(x), dengan f merupakan fungsi kontinu dan non negatif (f(x) ≥ 0) dalam interval a ≤ x ≤ b. Misalkan R adalah daerah yang dibatasi oleh kurva y = f(x), sumbu x, dan garis-garis x = a dan x = b. Luas daerah R dapat ditentukan dengan
$L = \int_{a}^{b} y dx$
Untuk lebih jelasnya berikut adalah contoh soal integral luas derah beserta pembahasannya
Contoh 1
Hitunglah luas daerah yang dibatasi oleh y = 3x$^2$ + 6x, sumbu x, dan garis-garis x = 0 dan y = 0!
Penyelesaian
L = $\int_{a}^{b} y dx$
L = $\int_{0}^{2} (3x^2 + 6x) dx$
L = $\int_{0}^{2} (x^3 + 3x) dx$
L = $[x^3 + 3x]\int_{0}^{2}$
L = $(2^3 + 3(2))-(0^3 + 3(0))$
L = (8 + 6) - 0
L = 14 satuan luas
Penjelasan di atas merupakan integal luas daerah kurva yang berada di atas sumbu x, bagaimana apabila ternyata luas daerah yang di cari berada di bawah sumbu-x? Perhatikan gambar berikut
Jika dihitung biasanya kita akan menemukan nilai luas negatif. Karena luas harus bernilai positif, maka rumus integral yang tepat untuk menghitung luas daerah tersebut adalah
$L = -\int_{a}^{b} y dx$
Berikut ini contoh integral luas daerah di bawah sumbu x beserta pembahasanya
Contoh 2
Hitunglah luas daerah yang dibatasi oleh kurva y = x$^2$ - 2x dan sumbu x!
Penyelesaian
Jika digambar maka luas daerah yang dimaksud adalah daerah yang berada di bawah kurva. Bagaimana dengan batas-batasnya? dalam hal ini batas atas dan batas bawah integral menggunakan titik potong sumbu x kurva tersebut.
0 = x$^2$ - 2x
(x - 2)x = 0
x - 2 = 0 atau x = 0
x = 2
L = $-\int_{a}^{b} y dx$
L = $-\int_{0}^{2}(x^2 - 2x) dx$
L = $-[\frac{1}{3}x^3 - x^2] \int_{0}^{2}$
L = $-((\frac{1}{3}(2)^3 - 2^2) - (\frac{1}{3}(0)^3 - 0^2))$
L = $-((\frac{8}{3} - 4) - (0))$
L = $-(\frac{8}{3} - \frac{12}{3})$
L = $-(- \frac{4}{3})$
L = $\frac{4}{3}$ satuan luas
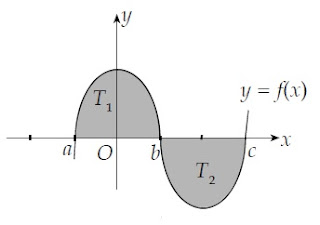
Pada kasus lain, luas daerah yang dicari berada di atas dan di bawah sumbu x. Perhatikan gambar berikut!
Untuk menentukan luas daerah tersebut kita dapat menggunakan rumus integral
$L = \int_{a}^{b} y dx$ $-\int_{b}^{c} y dx$
Perhatikan contoh soal berikut
Contoh 3
Tentukan luas daerah yang dibatasi oleh kurva y = x$^3$ - x dan sumbu x!
Penyelesaian
L = $\int_{a}^{b} y dx$ $-\int_{b}^{c} y dx$
L = $ [2x - \frac{1}{3}x^3- \frac{1}{2}x^2] \int_{-2}^{1}$
L = $ (2(1) - \frac{1}{3}(1)^3-\frac{1}{2}(1)^2)-(2(-2) - \frac{1}{3}(-2)^3 - \frac{1}{2}(-2)^2)$
L = $ (2 - \frac{1}{3} - \frac{1}{2})-(-4 + \frac{8}{3} - 2)$
L = $ ((\frac{7}{6})-(- \frac{20}{6})$
L = $ \frac{27}{6}$
Penyelesaian
Luas daerah yang dicari adalah luas daerah yang dibatasi oleh parabola dan sebuah garis, jadi kita dapat menggunakan cara cepat
2 - x$^2$ = -x
x$^2$ - x - 2 = 0
D = b$^2$ - 4ac = (-1)$^2$ - 4(1)(-2) = 9
L = $\frac{Dsqrt{D}}{6a^2}$
L = $\frac{9sqrt{9}}{6(1)^2}$
L = $\frac{9}{2}$ satuan luas
Contoh 7
Hitunglah luas daerah yang dibatasi oleh y = x$^2$ - 4 dan y = 8 - 2x$^2$!
Penyelesaian
Luas daerah yang dicari adalah luas daerah yang dibatasi oleh dua parabola, jadi kita dapat menggunakan cara cepat
x$^2$ - 4 = 8 - 2x$^2$
3x$^2$ - 12 = 0
D = = b$^2$ - 4ac = (0)$^2$ - 4(3)(-12) = 144
L = $\frac{Dsqrt{D}}{6a^2}$
L = $\frac{144sqrt{144}}{6(3)^2}$
L = $32$ satuan luas
Selain itu, pengembangan dari rumus cepat sebelumnya menghasilkan cara cepat menentukan luas daerah tanpa integral yang baru, yaitu
$L = \frac{a}{6}| x_1 - x_2 |^3$
x_1 dan x_2 merupakan titik potong kedua kurva. Karena rumus di atas merupakan pengembangan dari rumus pertama maka syarat rumus ini dapt digunakan juga sama yaitu luas yang dicari merupakan luas yang dibatasi oleh dua parabola atau luas yang dibatasi oleh parabola dan sebuah garis. Untuk lebih jelasnya perhatikan contoh berikut
Contoh 8
Tentukan luas daerah yang dibatasi oleh parabola y = 9 - x$^2$ dan y = x + 3!
Penyelesaian
9 - x$^2$ = x + 3
x$^2$ + x - 6 = 0
(x + 3)(x - 2) = 0
x$_1$ = -3 atau x$_2$ = 2
L = $\frac{a}{6}| x_1 - x_2 |^3$
L = $\frac{1}{6}| -3 - 2 |^3$
L = $\frac{1}{6}| -5 |^3$
L = $\frac{125}{6}$ satuan luas
Untuk memudahkan menentukan luas daerah dengan integral ada baiknya jika daerah tersebut digambar terlebih dahulu. Demikianlah tadi mengenai aplikasi integral tentu untuk menghitung luas daerah yang telah dilengkapi pembahasanya. Semoga bermanfaat.
Pada bahasan kali ini kita akan membahas mengenai aplikasi integral untuk menghitung luas daerah. Luas daerah yang dimaksud dalam hal ini adalah luas daerah yang dibatasi oleh kurva dengan sumbu x dan luas daerah yang dibatasi oleh dua kurva
Luas Daerah yang Dibatasi oleh Kurva dan Sumbu x
$L = \int_{a}^{b} y dx$
Untuk lebih jelasnya berikut adalah contoh soal integral luas derah beserta pembahasannya
Contoh 1
Hitunglah luas daerah yang dibatasi oleh y = 3x$^2$ + 6x, sumbu x, dan garis-garis x = 0 dan y = 0!
Penyelesaian
L = $\int_{a}^{b} y dx$
L = $\int_{0}^{2} (3x^2 + 6x) dx$
L = $\int_{0}^{2} (x^3 + 3x) dx$
L = $[x^3 + 3x]\int_{0}^{2}$
L = $(2^3 + 3(2))-(0^3 + 3(0))$
L = (8 + 6) - 0
L = 14 satuan luas
Penjelasan di atas merupakan integal luas daerah kurva yang berada di atas sumbu x, bagaimana apabila ternyata luas daerah yang di cari berada di bawah sumbu-x? Perhatikan gambar berikut
$L = -\int_{a}^{b} y dx$
Berikut ini contoh integral luas daerah di bawah sumbu x beserta pembahasanya
Contoh 2
Hitunglah luas daerah yang dibatasi oleh kurva y = x$^2$ - 2x dan sumbu x!
Penyelesaian
Jika digambar maka luas daerah yang dimaksud adalah daerah yang berada di bawah kurva. Bagaimana dengan batas-batasnya? dalam hal ini batas atas dan batas bawah integral menggunakan titik potong sumbu x kurva tersebut.
0 = x$^2$ - 2x
(x - 2)x = 0
x - 2 = 0 atau x = 0
x = 2
L = $-\int_{a}^{b} y dx$
L = $-\int_{0}^{2}(x^2 - 2x) dx$
L = $-[\frac{1}{3}x^3 - x^2] \int_{0}^{2}$
L = $-((\frac{1}{3}(2)^3 - 2^2) - (\frac{1}{3}(0)^3 - 0^2))$
L = $-((\frac{8}{3} - 4) - (0))$
L = $-(\frac{8}{3} - \frac{12}{3})$
L = $-(- \frac{4}{3})$
L = $\frac{4}{3}$ satuan luas
Pada kasus lain, luas daerah yang dicari berada di atas dan di bawah sumbu x. Perhatikan gambar berikut!
$L = \int_{a}^{b} y dx$ $-\int_{b}^{c} y dx$
Perhatikan contoh soal berikut
Contoh 3
Tentukan luas daerah yang dibatasi oleh kurva y = x$^3$ - x dan sumbu x!
Penyelesaian
Titik potong kurva dengan sumbu x adalah
0 = x$^3$ - x
x(x + 1)(x - 1) = 0
x = -1 atau x = 0 atau x = 1
Jika digambar maka kurvanya akan terlihat seperti berikut
L = $\int_{-1}^{0} (x $^3$ - x) dx$ $-\int_{0}^{1} (x $^3$ - x) dx$
L = $ [\frac{1}{4}x $^4$ - \frac{1}{2}x^2] \int_{-1}^{0}$ $- [\frac{1}{4}x $^4$ - \frac{1}{2}x^2] \int_{0}^{1}$
L = $ ((\frac{1}{4}(0) $^4$ - \frac{1}{2}(0)^2)-(\frac{1}{4}(-1) $^4$ - \frac{1}{2}(-1)^2))$ $- ((\frac{1}{4}(1) $^4$ - \frac{1}{2}(1)^2)-(\frac{1}{4}(0) $^4$ - \frac{1}{2}(0)^2))$
L = $ (0 -(-\frac{1}{4}))$ $- ((- \frac{1}{4}) - 0)$
L = $ \frac{1}{4}$ $+ \frac{1}{4}$
L = $ \frac{1}{2}$ satuan luas
Misalkan dua kurva masing-masing y = f(x) dan y = g(x), merupakan kurva-kurva yang kontinu dan f(x) ≥ g(x) dalam interval a ≤ x ≤ b. Daerah yang dibatasi oleh kurva y = f(x), dan y = g(x), garis x = a, dan garis x = b luasnya dapat ditentukan oleh rumus integral
$L = \int_{a}^{b} [f(x) - g(x)] dx$
Berikut adalah contoh soal beserta pembahasannya
Contoh 4
Tentkan luas daerah yang dibatasi oleh kurva parabola y = 2 - x$^2$ dan garis y = x!
Penyelesaian
Terlebih dahulu kita mencari batas-batas integralnya, yaitu
2 - x$^2$ = x
x$^2$ + x - 2 = 0
(x + 2)(x - 1) = 0
x = -2 zatau x = 1
L = $\int_{-2}^{1} [(2 - x^2) - x] dx$L = $ [\frac{1}{4}x $^4$ - \frac{1}{2}x^2] \int_{-1}^{0}$ $- [\frac{1}{4}x $^4$ - \frac{1}{2}x^2] \int_{0}^{1}$
L = $ ((\frac{1}{4}(0) $^4$ - \frac{1}{2}(0)^2)-(\frac{1}{4}(-1) $^4$ - \frac{1}{2}(-1)^2))$ $- ((\frac{1}{4}(1) $^4$ - \frac{1}{2}(1)^2)-(\frac{1}{4}(0) $^4$ - \frac{1}{2}(0)^2))$
L = $ (0 -(-\frac{1}{4}))$ $- ((- \frac{1}{4}) - 0)$
L = $ \frac{1}{4}$ $+ \frac{1}{4}$
L = $ \frac{1}{2}$ satuan luas
Luas Daerah yang Dibatasi Dua Kurva
$L = \int_{a}^{b} [f(x) - g(x)] dx$
Berikut adalah contoh soal beserta pembahasannya
Contoh 4
Tentkan luas daerah yang dibatasi oleh kurva parabola y = 2 - x$^2$ dan garis y = x!
Penyelesaian
Terlebih dahulu kita mencari batas-batas integralnya, yaitu
2 - x$^2$ = x
x$^2$ + x - 2 = 0
(x + 2)(x - 1) = 0
x = -2 zatau x = 1
L = $ [2x - \frac{1}{3}x^3- \frac{1}{2}x^2] \int_{-2}^{1}$
L = $ (2(1) - \frac{1}{3}(1)^3-\frac{1}{2}(1)^2)-(2(-2) - \frac{1}{3}(-2)^3 - \frac{1}{2}(-2)^2)$
L = $ (2 - \frac{1}{3} - \frac{1}{2})-(-4 + \frac{8}{3} - 2)$
L = $ ((\frac{7}{6})-(- \frac{20}{6})$
L = $ \frac{27}{6}$
L = $ \frac{9}{2}$ satuan luas
Contoh 5
Hitunglah luas daerah yang dibatasi oleh kurva y = 6x - x$^2$ dan y = x$^2$!
Penyelesaian
6x - x$^2$ = x$^2$
2x$^2$ - 6x = 0
x(2x - 6) = 0
x = 0 atau x = 3
L = $\int_{0}^{3} [6x - x^2 - x^2] dx$
L = $\int_{0}^{3} [6x - 2x^2] dx$
L = $ [3x^2 - \frac{2}{3}x^3] \int_{0}^{3}$
L = $ ((3(3)^2 - \frac{2}{3}(3)^3) - ((3(0)^2 - \frac{2}{3}(0)^3)$
L = $ ((27 - 18) - (0 - 0)$
L = 9 satuan luas
Cara Cepat Menentukan Luas Daerah yang Dibatasi Dua Kurva
Sebenarnya ada cara cepat yang dapat digunakan untuk menentukan luas daerah yang dibatasi dua kurva tanpa menggunakan integral. Namun, ada kondisi khusus atau syarat yang harus dipenuhi yaitu luas yang dicari merupakan luas yang dibatasi oleh dua parabola atau luas yang dibatasi oleh parabola dan sebuah garis. Untuk menentukan luasnya, kita dapat menggunakan rumus
$L = \frac{Dsqrt{D}}{6a^2}
D sendiri adalah diskriminan dan D = b$^2$ - 4ac. Diskriminan diperoleh dengan cara mensubstitusi salah satu kurva ke kurva yang lain sehingga diperoleh persamaan ax$^2$ + bx + c = 0. Untuk lebih jelasnya perhatikan contoh soal menentukan luas daerah tanpa integral beserta pembahasannya
Contoh 6
Hitunglah luas daerah yang dibatasi oleh y = 2 - x$^2$ dan y = -x!Penyelesaian
Luas daerah yang dicari adalah luas daerah yang dibatasi oleh parabola dan sebuah garis, jadi kita dapat menggunakan cara cepat
2 - x$^2$ = -x
x$^2$ - x - 2 = 0
D = b$^2$ - 4ac = (-1)$^2$ - 4(1)(-2) = 9
L = $\frac{Dsqrt{D}}{6a^2}$
L = $\frac{9sqrt{9}}{6(1)^2}$
L = $\frac{9}{2}$ satuan luas
Contoh 7
Hitunglah luas daerah yang dibatasi oleh y = x$^2$ - 4 dan y = 8 - 2x$^2$!
Penyelesaian
Luas daerah yang dicari adalah luas daerah yang dibatasi oleh dua parabola, jadi kita dapat menggunakan cara cepat
x$^2$ - 4 = 8 - 2x$^2$
3x$^2$ - 12 = 0
D = = b$^2$ - 4ac = (0)$^2$ - 4(3)(-12) = 144
L = $\frac{Dsqrt{D}}{6a^2}$
L = $\frac{144sqrt{144}}{6(3)^2}$
L = $32$ satuan luas
Selain itu, pengembangan dari rumus cepat sebelumnya menghasilkan cara cepat menentukan luas daerah tanpa integral yang baru, yaitu
$L = \frac{a}{6}| x_1 - x_2 |^3$
x_1 dan x_2 merupakan titik potong kedua kurva. Karena rumus di atas merupakan pengembangan dari rumus pertama maka syarat rumus ini dapt digunakan juga sama yaitu luas yang dicari merupakan luas yang dibatasi oleh dua parabola atau luas yang dibatasi oleh parabola dan sebuah garis. Untuk lebih jelasnya perhatikan contoh berikut
Contoh 8
Tentukan luas daerah yang dibatasi oleh parabola y = 9 - x$^2$ dan y = x + 3!
Penyelesaian
9 - x$^2$ = x + 3
x$^2$ + x - 6 = 0
(x + 3)(x - 2) = 0
x$_1$ = -3 atau x$_2$ = 2
L = $\frac{a}{6}| x_1 - x_2 |^3$
L = $\frac{1}{6}| -3 - 2 |^3$
L = $\frac{1}{6}| -5 |^3$
L = $\frac{125}{6}$ satuan luas
Untuk memudahkan menentukan luas daerah dengan integral ada baiknya jika daerah tersebut digambar terlebih dahulu. Demikianlah tadi mengenai aplikasi integral tentu untuk menghitung luas daerah yang telah dilengkapi pembahasanya. Semoga bermanfaat.
