Dalam bahasan kali ini, akan dibahas mengenai sistem pertidaksamaan linear dua variabel. Sistem pertidaksamaan linear dua variabel merupakan bagian dari penyelesaian masalah program linear. Sehingga sangat penting untuk memahami materi ini terlebih dahulu sebelum mempelajari program linear. Sistem pertidaksamaan linear dua variabel tentu sangat berbeda dengan sistem persamaan linear dua variabel. Selain, perbedaan tanda hubung yang dimiliki oleh keduanya. Bentuk penyelesaian dan metode penyelesaiannya juga tidak sama. Nah, untuk lebih jelasnya mengenai sistem pertidaksamaan linear simaklah ulasan berikut.

berikut adalah contohnya
2x + 3y > 6
4x - y < 9
Berbeda dengan penyelesaian dari persamaan linear dua variabel yang berupa himpunan pasangan titik-titik atau jika digambar grafiknya akan berupa garis lurus, penyelesaian pertidaksamaan linear dua variabel berua daerah penyelesaian. Dalam praktiknya penyelesaian pertidaksamaan linear dapat berupa daerah diarsir atau sebaliknya daerah penyelesaian pertidaksamaan linear dua variabel berupa daerah bersih.
Untuk menentukkan daerah penyelesaiannya, dapat dilakukan melalui langkah-langkah berikut.
Untuk lebih jelasnya perhatikan contoh berikut
Contoh 1
Tentukan daerah penyelesaian dari pertidaksamaan linear dua variabel berikut
a. 3x + y < 9
b. 4x - 3y ≥ 24
Penyelesaian
a. 3x + y < 9
3x + y = 9

Grafik Penyelesaian
(Garis putus-putus digunakan menunjukkan tanda ketidaksamaan < atau > dengan kata lain tanda ketidaksamaan tanpa sama dengan)
Uji titik (0, 0)
3(0) + 0 < 9
0 < 9 (benar)
Karena pernyataannya menjadi benar, maka (0, 0) termasuk penyelesaianya. Sehingga daerah yang memuat (0, 0) merupakan penyelesaianya. Dalam hal ini yang daerah bersih merupakan penyelesaian dari pertidaksamaan.
b. 4x - 3y ≥ 24
4x - 3y = 24

Grafik Penyelesaian
Uji titik (0, 0)
4(0) - 3(0) ≥ 24
0 ≥ 24 (salah)
Karena pernyataanya menjadi salah, maka (0, 0) bukan termasuk penyelesaianya. Sehingga daerah penyelesainnya tidak memuat (0, 0) dan daerah bersihnya (daerah penyelesaian) berada di bawah garis.
Untuk melakukan uji titik, tidak harus selalu menggunakkan titik (0, 0). Titik mana saja bisa digunakan asalkan titik tersebut tidak dilalui oleh garis persamaan. Pada dua contoh di atas, dasar pertimbangan menggunakan titik (0, 0) adalah selain tidak dilalui oleh garis serta mempermudah perhitungan.
Contoh 2
Tentukan daerah penyelesaian dari sistem pertidaksamaan dua variabel berikut!
x + y ≤ 9
6x + 11 y ≤ 66
x ≥ 0
y ≥ 0
Penyelesaian
x + y ≤ 9
x + y = 9

6x + 11 y ≤ 66
6x + 11 y = 66

x ≥ 0, gambar garisnya berimpit dengan sumbu y dengan daerah penyelesaian di kanan sumbu y
y ≥ 0, gambar garisnya berimpit dengan sumbu x dengan daerah penyelesaian di atas sumbu x
Grafik Penyelesaian
Uji titik (0, 0)
0 + 0 ≤ 9
0 ≤ 9 (benar)
Uji titik (0, 0)
6(0) + 11(0) ≤ 66
0 ≤ 66 (benar)
Contoh 3
Tentukan daerah penyelesaian dari sistem pertidaksamaan dua variabel berikut!
x + y ≤ 5
4x + 6 y ≤ 24
x ≥ 1
y ≥ 2
Penyelesaian
x + y ≤ 5
x + y = 5
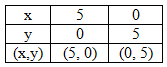
4x + 6 y ≤ 24
4x + 6 y = 24

x ≥ 1, gambar garisnya melalui x = 1 dan sejajar sumbu y dengan daerah penyelesaian di kanan garis
y ≥ 2, gambar garisnya melalui y = 2 dan sejajar sumbu x dengan daerah penyelesaian di atas garis
Grafik Penyelesaian
Uji titik (0, 0)
0 + 0 ≤ 9
0 ≤ 9 (benar)
Uji titik (0, 0)
6(0) + 11(0) ≤ 66
0 ≤ 66 (benar)
Demikianlah mengenai Sistem Pertidaksamaan Linear Dua Variabel, semoga dapat dipahami dan bermanfaat.

Pertidaksamaan Linear Dua Variabel
Sebelum membahas mengenai sistem pertidaksamaan linear dua variabel, terlebih dahulu kita mempelajari mengenai pertidaksamaan linear dua variabel. Pertidaksamaan linear dua variabel adalah kalimat terbuka matematika yang memuat dua variabel, dengan masing-masing variabel berderajat satu dan dihubungkan dengan tanda ketidaksamaan. Tanda ketidaksamaan yang dimaksud adalah >, <, ≤, atau ≥. Sehingga bentuk pertidaksamaan linear dapat dituliskan sebagai berikut.ax + by > c
ax + by < c
ax + by ≥ c
ax + by ≤ c
berikut adalah contohnya
2x + 3y > 6
4x - y < 9
Berbeda dengan penyelesaian dari persamaan linear dua variabel yang berupa himpunan pasangan titik-titik atau jika digambar grafiknya akan berupa garis lurus, penyelesaian pertidaksamaan linear dua variabel berua daerah penyelesaian. Dalam praktiknya penyelesaian pertidaksamaan linear dapat berupa daerah diarsir atau sebaliknya daerah penyelesaian pertidaksamaan linear dua variabel berupa daerah bersih.
Untuk menentukkan daerah penyelesaiannya, dapat dilakukan melalui langkah-langkah berikut.
- Ubahlah tanda ketidaksamaan dari pertidaksamaan menjadi tanda sama dengan (=), sehingga diperoleh persamaan linear dua variabel
- Lukis grafik/garis dari persamaan linear dua variabel tadi. Hal ini dapat dilakukan dengan menentukan titik potong sumbu x dan sumbu y dari persamaan atau menggunakan dua titik sembarang yang dilalui oleh garis. Garis akan membagi dua bidang kartesius
- Lakukan uji titik yang tidak dilalui oleh garis (substitusi nilai x dan y titik ke pertidaksamaan). Jika menghasilkan pernyataan yang benar, artinya daerah tersebut merupakan penyelesaiannya, namun apabila menghasilkan pernyataan salah maka bagian lainnya lah yang merupakan penyelesaiaanya.
Untuk lebih jelasnya perhatikan contoh berikut
Contoh 1
Tentukan daerah penyelesaian dari pertidaksamaan linear dua variabel berikut
a. 3x + y < 9
b. 4x - 3y ≥ 24
Penyelesaian
a. 3x + y < 9
3x + y = 9

Grafik Penyelesaian
(Garis putus-putus digunakan menunjukkan tanda ketidaksamaan < atau > dengan kata lain tanda ketidaksamaan tanpa sama dengan)
Uji titik (0, 0)
3(0) + 0 < 9
0 < 9 (benar)
Karena pernyataannya menjadi benar, maka (0, 0) termasuk penyelesaianya. Sehingga daerah yang memuat (0, 0) merupakan penyelesaianya. Dalam hal ini yang daerah bersih merupakan penyelesaian dari pertidaksamaan.
b. 4x - 3y ≥ 24
4x - 3y = 24

Grafik Penyelesaian
Uji titik (0, 0)
4(0) - 3(0) ≥ 24
0 ≥ 24 (salah)
Karena pernyataanya menjadi salah, maka (0, 0) bukan termasuk penyelesaianya. Sehingga daerah penyelesainnya tidak memuat (0, 0) dan daerah bersihnya (daerah penyelesaian) berada di bawah garis.
Untuk melakukan uji titik, tidak harus selalu menggunakkan titik (0, 0). Titik mana saja bisa digunakan asalkan titik tersebut tidak dilalui oleh garis persamaan. Pada dua contoh di atas, dasar pertimbangan menggunakan titik (0, 0) adalah selain tidak dilalui oleh garis serta mempermudah perhitungan.
Sistem Pertidaksamaan Linear Dua Variabel
Sistem pertidakasamaan linear dua variabel adalah sistem pertidaksamaan yang melibatkan dua atau lebih pertidaksamaan linear dua variabel. Daerah penyelesaian dari sistem pertidaksamaan linear dua variabel merupakan daerah yang memenuhi semua pertidaksamaan yang ada dalam sistem. Untuk lebih jelasnya perhatikan contoh berikutContoh 2
Tentukan daerah penyelesaian dari sistem pertidaksamaan dua variabel berikut!
x + y ≤ 9
6x + 11 y ≤ 66
x ≥ 0
y ≥ 0
Penyelesaian
x + y ≤ 9
x + y = 9

6x + 11 y ≤ 66
6x + 11 y = 66

x ≥ 0, gambar garisnya berimpit dengan sumbu y dengan daerah penyelesaian di kanan sumbu y
y ≥ 0, gambar garisnya berimpit dengan sumbu x dengan daerah penyelesaian di atas sumbu x
Grafik Penyelesaian
Uji titik (0, 0)
0 + 0 ≤ 9
0 ≤ 9 (benar)
Uji titik (0, 0)
6(0) + 11(0) ≤ 66
0 ≤ 66 (benar)
Contoh 3
Tentukan daerah penyelesaian dari sistem pertidaksamaan dua variabel berikut!
x + y ≤ 5
4x + 6 y ≤ 24
x ≥ 1
y ≥ 2
Penyelesaian
x + y ≤ 5
x + y = 5

4x + 6 y ≤ 24
4x + 6 y = 24

x ≥ 1, gambar garisnya melalui x = 1 dan sejajar sumbu y dengan daerah penyelesaian di kanan garis
y ≥ 2, gambar garisnya melalui y = 2 dan sejajar sumbu x dengan daerah penyelesaian di atas garis
Grafik Penyelesaian
Uji titik (0, 0)
0 + 0 ≤ 9
0 ≤ 9 (benar)
Uji titik (0, 0)
6(0) + 11(0) ≤ 66
0 ≤ 66 (benar)
Demikianlah mengenai Sistem Pertidaksamaan Linear Dua Variabel, semoga dapat dipahami dan bermanfaat.




