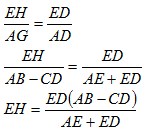Pada artikel sebelumnya kita telah membahas mengenai Rumus Menentukan Jarak Titik Tengah dari Kedua Diagonal Trapesium. Artikel kali ini juga akan membahas mengenai trapesium yaitu mengenai cara menentukan panjang EF yang merupakan salah satu garis sejajar dari suatu Trapesium. Saya sengaja memberi judul secara spesifik seperti itu yaitu menentukan panjang EF, karena kebanyakan sumber-sumber yang saya baca baik buku maupun soal-soal yang saya temukan lebih familiar menyebutkan panjang EF. Lantas, garis manakah yang dinamakan EF dalam suatu trapesium?
Untuk menjawab pertanyaan di atas perhatikan gambar trapesium berikut
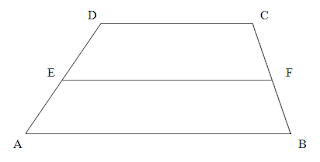
Gambar di atas merupakan gambar sebuah trapesium ABCD, dengan panjang sisi sejajar AB dan CD, titik E dan F merupakan titik yang berturut-turut berada pada garis AB dan CD dan EF merupakan garis yang sejajar dengan garis AB dan CD.
Untuk menemukan rumus panjang EF, kita dapat melakukannya dengan cara yang akan dijelaskan pada paragraf berikut ini. Namun, sebelumnya perlu diingat bahwa agar lebih mudah memahami penjelasan yang akan diberikan anda setidaknya telah memahami sedikit tentang materi kesebangunan pada segitiga.
Pada trapesium sembarang ABCD, misalkan terdapat titik G yang merupakan titik yang terletak pada garis AB dengan panjang GB sama dengan panjang CD (GD = CD). Sehingga garis GD sejajar dengan garis BC (GD//BC). Titik H merupakan titik potong garis GD dengan garis EF, dimana panjang HF sama dengan panjang CD (HF = CD).
Dari gambar di atas pula didapat bahwa
AF = HF + EH
AF = CD + EH
Perhatikan gambar di atas kembali segitiga AGD sebangun dengan segitiga EHD (AGD ~ EHD). Dari kesebangunan tersebut diperoleh perbandingan panjang sisi-sisi yang bersesuaian adalah
Yang dipakai dalam menentukkan rumus adalah
Dari bentuk perbandingan di atas diperoleh
Dengan demikian dapat disimpulkan bahwa untuk menentukkan panjang EF dapat menggunakan rumus berikut
Untuk menjawab pertanyaan di atas perhatikan gambar trapesium berikut
Gambar di atas merupakan gambar sebuah trapesium ABCD, dengan panjang sisi sejajar AB dan CD, titik E dan F merupakan titik yang berturut-turut berada pada garis AB dan CD dan EF merupakan garis yang sejajar dengan garis AB dan CD.
Untuk menemukan rumus panjang EF, kita dapat melakukannya dengan cara yang akan dijelaskan pada paragraf berikut ini. Namun, sebelumnya perlu diingat bahwa agar lebih mudah memahami penjelasan yang akan diberikan anda setidaknya telah memahami sedikit tentang materi kesebangunan pada segitiga.
Pada trapesium sembarang ABCD, misalkan terdapat titik G yang merupakan titik yang terletak pada garis AB dengan panjang GB sama dengan panjang CD (GD = CD). Sehingga garis GD sejajar dengan garis BC (GD//BC). Titik H merupakan titik potong garis GD dengan garis EF, dimana panjang HF sama dengan panjang CD (HF = CD).
Dari gambar di atas pula didapat bahwa
AF = HF + EH
AF = CD + EH
Perhatikan gambar di atas kembali segitiga AGD sebangun dengan segitiga EHD (AGD ~ EHD). Dari kesebangunan tersebut diperoleh perbandingan panjang sisi-sisi yang bersesuaian adalah
Yang dipakai dalam menentukkan rumus adalah
Dari bentuk perbandingan di atas diperoleh
Sehingga, panjang EF ditentukan dengan cara
$EF$ =$CD + \frac{ED(AB - CD)}{AE + ED}$
$EF$ =$\frac{CD(AE + ED)}{AE + ED}$ + $\frac{ED(AB - CD)}{AE + ED}$
$EF$ =$ \frac{CD.AE + CD.ED +ED.AB - ED.CB}{AE + ED}$
$EF$ = $\frac{CD.AE + ED.AB}{AE + ED}$
Dengan demikian dapat disimpulkan bahwa untuk menentukkan panjang EF dapat menggunakan rumus berikut
$EF$ = $\frac{CD.AE + ED.AB}{AE + ED}$
Semoga bermanfaat